计算机系统硬件
你的支持是君哥更新的动力
软考笔记 加入君哥微信粉丝群:coding178 备注:架构 点击观看全套视频
本章知识概览:
计算机结构、CPU 组成、冯·诺依曼结构与哈佛结构、嵌入式芯片、存储系统、层次化存储结构、Cache、主存编址、磁盘管理、磁盘调度、数据传输控制方式、总线、CISC与RISC、流水线、校验码、奇偶校验、循环校验码CRC
计算机系统基础知识
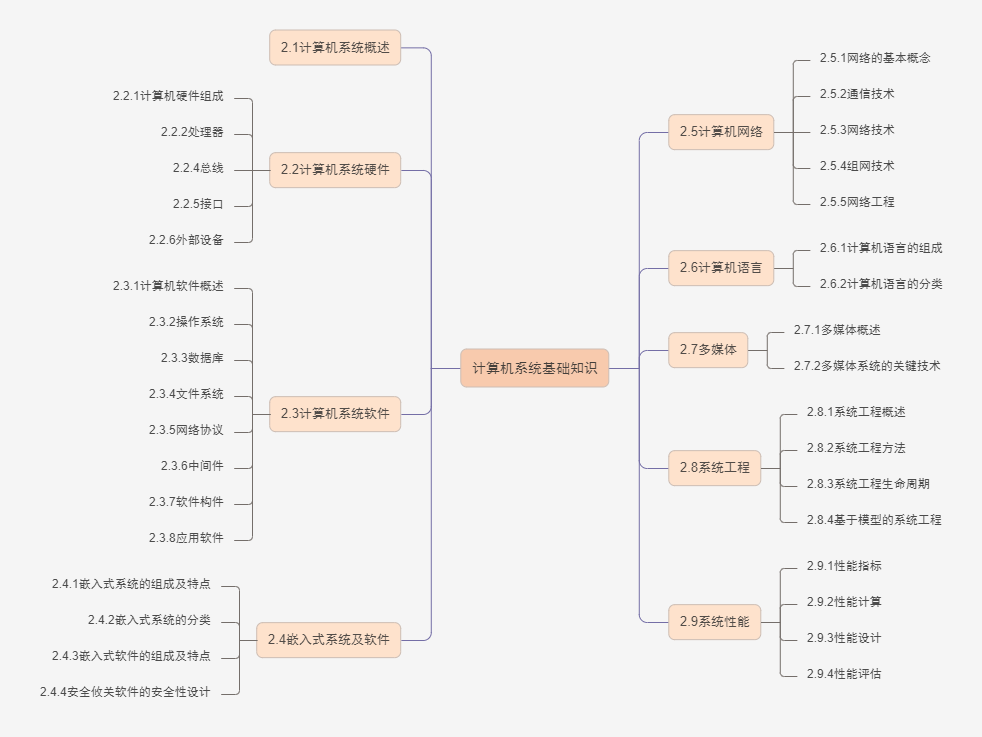
计算机组成结构Computer Architecture
计算机硬件组成
运算器、控制器、存储器、输入设备、输出设备(运控纯输出)
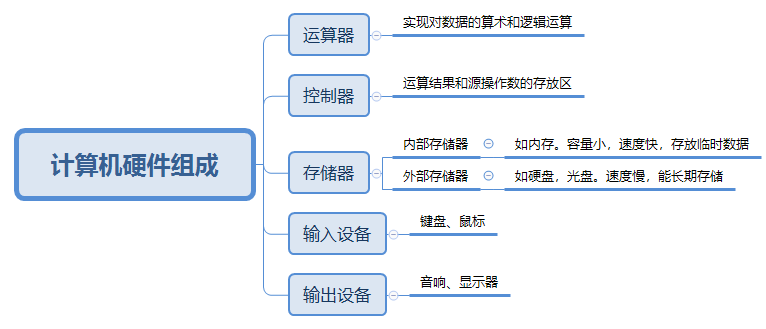
存储器是记忆设备,分为内部存储器和外部存储器
- 内部存储器:(即内存、容量小、速度快、一般用于临时存放数据或中间结果)
- 外部存储器:(除计算机内存及CPU缓存以外的储存器,即本地磁盘、光盘等、容量大、速度慢、长期保存数据)
输入设备和输出设备合并称为外部设备,即外设。
- 输入设备:原始数据或命令的输入(键盘、鼠标、麦克风、扫描仪)
- 输出设备:计算机运行的结果(显示器、扬声器)
运算器和控制器等部件被集成在一起统称为中央处理单元。
中央处理单元Central Processing Unit
CPU
CPU组成与功能
组成:运算器、控制器、寄存器组、内部总线 功能:和我们的人脑一样,可以完成算术、数据加工处理、逻辑运算和控制(程序控制、操作控制、时间控制),一句话“能算能控“
在计算机数据存储中,存储数据的基本单位是字节(byte),1 字节等于 8 位(8 bit)。每一个字节都对应一个内存地址。
我们常说的32 位和 64 位通常称为 CPU 的位宽,代表的是 CPU 一次可以计算的数据量 。最主要区别在于一次能计算多少字节数据:
32 位 CPU 一次可以计算 4 个字节;
64 位 CPU 一次可以计算 8 个字节;
寄存器组了解分类
- 专用寄存器:运算器和控制器中的寄存器是专用寄存器,其作用是固定的。
- 通用寄存器:用途广泛并可由程序员规定其用途,其数目因处理器不同而不同。
运算器
负责运算从内存读入寄存器的数据,如加减乘除,与或非比较等运算
- 算术逻辑单元ALU
Arithmetic Logic Unit(实现对数据的算术和逻辑运算) - 累加寄存器AC
Accumulator简称累加器(存放运算结果或源操作数)- 累加器是一种通用寄存器,其功能是:当运算器的ALU执行算术逻辑运算时,为其提供一个工作区。累加器暂时存放ALU运算的结果信息。运算器中至少需要一个累加寄存器。
- 数据缓冲寄存器DR
Data Register(写内存时,暂存内存的指令或数据,作为CPU和内存, 外部设备之间的数据传送中转站,用以弥补CPU和主存、外设之间操作速度上的差异。) - 程序状态字PSW 又名(程序状态字寄存器
program status word)(保存指令运行结果的条件码内容,如溢出标志O、负标志N、进/借位标志C等)
控制器
它是计算机指挥系统,负责协调并且控制计算机各部件执行程序的指令序列,调度运算器把计算做好,把内存上的指令、数据等读入寄存器。包括取指令(形成指令地址)、分析指令(操作码译码,产生操作数有效地址)和执行指令(控制设备,发出有关操作控制信号)。由程序计数器、指令寄存器、指令译码器、时序产生器(Timing Generator)、操作控制器(Control Unit)组成。
什么是指令
一条指令就是机器语言的一个语句,它是一组有意义的二进制代码。
程序计数器PC
Program Counter Register(存放的是将要执行的指令地址,这个地址是从地址寄存器中获取的)地址寄存器AR
Address Register又称指令地址寄存器(保存当前CPU所访问的内存单元的地址。由于内存和CPU存在速度上的差异,所以需要使用AR保存地址信息,直到内存读/写操作完成为止。)指令寄存器IR
Instruction Register(暂存CPU执行指令,由指令译码器根据指令寄存器中的内容产生各种微操作指令,控制其他部分协调工作)指令译码器ID
Instruction Decoder(分析指令操作码,每条指令执行之前必须先分析该指令的操作码是什么,然后向操作控制器发出具体的控制信号。)操作控制器与时序产生器:数据通路是许多寄存器之间传送信息的通路。 信息从什么地方开始,中间经过哪个寄存器或多路开关,最后传送到哪个寄存器,都要加以控制。 在各寄存器之间建立数据通路的任务,是由称为操作控制器的部件来完成的。
操作控制器的功能:就是根据指令操作码和时序信号,产生各种操作控制信号,以便正确地建立数据通路,从而完成取指令和执行指令的控制。
内部总线了解分类
内部总线是一种内部结构,是CPU、内存、输入、输出设备传递信息的公用通道。
- 数据总线(DB):用来传送数据信息,是双向的。DB的宽度决定了CPU和计算机其他设备之间每次交换数据的位数。
- 地址总线(AB):用于传送CPU发出的地址信息,由于地址只能从CPU传向外部存储器或I/O端口,所以地址总线总是单向三态的,这与数据总线不同,地址总线的位数决定了CPU可直接寻址的内存空间大小(寻址能力)。
- 控制总线(CB):用来传送控制信号、时序信号和状态信息等。CB中的每一条线的信息传送方向是单方向且确定的,但CB作为一个整体则是双向的。
当 CPU 要读写内存数据的时候,一般需要通过下面这三个总线:
首先要通过「AB」来指定内存的地址;
然后通过「CB」控制是读或写命令;
最后通过「DB」来传输数据;
冯·诺依曼和哈佛结构
概述
冯.诺伊曼结构(von Neumann architecture),也称普林斯顿结构,最早由冯·诺依曼于1945年提出。是一种将程序指令存储器和数据存储器并在一起的存储器结构。它的主要特点如下:
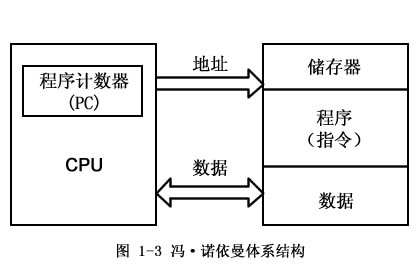
- 指令和数据存储在同一个存储器中,共享同一个存储器。
- 使用单一的地址总线和数据总线来传输数据和指令。
- 一个CPU核心同时只能执行一条指令。
取指令和存取数据要从同一个存储空间存取,经由同一总线传输,因而它们无法重叠执行,只有一个完成后再进行下一个。
哈佛(Harvard)结构由哈佛大学教授霍华德·艾肯和霍尔曼·威尔士于20世纪40年代开发的,是一种将程序指令存储和数据存储分开的存储器结构。它的主要特点如下:
- 将程序和数据存储在不同的存储空间中,即程序存储器和数据存储器是两个相互独立的存储器,每个存储器独立编址、独立总线传输,并行处理。
- 一个CPU核心可以同时执行多条指令。
- 哈佛结构的高速缓存与数据存储器独立,减少了缓存读写之间的竞争,更有效地提高了缓存命中率。
有4条总线,程序的数据总线与地址总线,数据的数据总线与地址总线。这种分离的程序总线和数据总线可允许在一个机器周期内同时获取指令字(来自程序存储器)和操作数(来自数据存储器),从而提高了执行速度,使数据的吞吐率提高了1倍。又由于程序和数据存储器在两个分开的物理空间中,因此取指和执行能完全重叠。
哈佛架构多用于一些嵌入式系统等领域。普通人一般接触不到它。
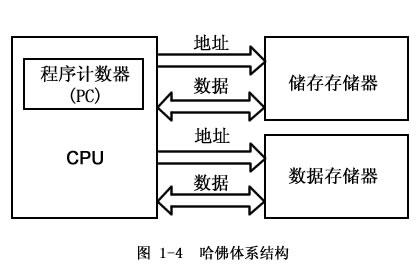
一句话总结:二者的区别在于在于 CPU 与内存的存取方式,即程序空间与数据空间是否为一体。再通俗一点,诺曼架构是盖浇饭,一个篮子里面混放了饭和菜,一次只能拿一样。哈佛结构是单独的篮子放饭和菜,且可以同时拿饭和菜。
缺点
诺依曼
- 同时传输数据和指令,导致存储器和处理器之间的效率低下。
- 存储器中的指令和数据被混合存储,指令可以被当作数据进行处理,因此程序可以动态地修改自身代码,容易受到病毒、恶意程序等攻击。
- 指令和数据必须具有相同的位宽。
哈佛
- 指令与数据传输同时运行,运行效率高。
- 存储器中的指令和数据分开存储,因此程序无法直接修改自身代码,这样会更加安全可靠、固若金汤。
- 指令和数据的位宽可以不同。
应用场景
天下没有完美的事情,效率高的设计和实现肯定要复杂,所以他们都有合适于自己的使用场景。
冯·诺依曼结构一般用于PC处理器,例如
i5,i7,i9处理器哈佛结构一般用于嵌入式系统、
DSP、FPGA、网络处理器等领域(哈佛结构的并行处理能力使其特别适合于需要同时处理多个数据流的计算,如高能物理实验数据的处理和分析、天文学中对海量星象数据进行处理和质量选取等)。
嵌入式处理器可分为以下4大类
- 嵌入式数字信号处理器
(Digital Signal Processor)DSP: - 嵌入式微控制单元或微控制器
(Micro Controller Unit)MCU - 嵌入式片上系统
(System On Chip)SOC - 嵌入式处理器
(Micro Processor Unit)MPU
| 定义 | 简述 | 用途 | |
|---|---|---|---|
| DSP | 专门用于信号处理方面的处理器 | 常用于数字信号、音频编解码、滤波等应用。具有专门的硬件乘法器,广泛采用流水线操作,提供特殊的DSP指令,可以用来快速的实现各种数字信号处理算法。 | |
| MCU | 把计算机阉割版的CPU和RAM、ROM、定时器和其他外设集成在一个芯片上,形成芯片级的计算机,注重控制。MCU没有Cache(缓存)和MMU(内存管理单元)。 | 单片机(Single-Chip,缩小版人) | 用于简单的控制场景,例如家电控制、汽车电子、医疗设备、工业自动化、物联网(IoT)设备等。ARM的Cortex-M系列芯片 |
| SOC | 将CPU与其他外设集成到芯片里,即集成度更高的CPU。MCU只是芯片级的芯片。而SOC是系统级的芯片,它集成了MCU和MPU的优点。 | 微小型系统(把系统做到芯片上) | 用于通用计算和多媒体处理,例如手机、平板电脑和智能音箱,通常跑Linux或Android系统。高通、骁龙、海思等处理器都是SOC。 |
| MPU | 通常代表功能强大的CPU(可理解为增强型的CPU)但不是为任何已有的特定计算目的而设计的芯片。这种芯片往往是个人计算机和高端工作站的核心CPU。 | 微处理器(缩小版大脑) | 最常见的微处理器是Motorola的68K系列和Intel的X86系列。ARM的Cortex-A系列芯片 |
多核CPU
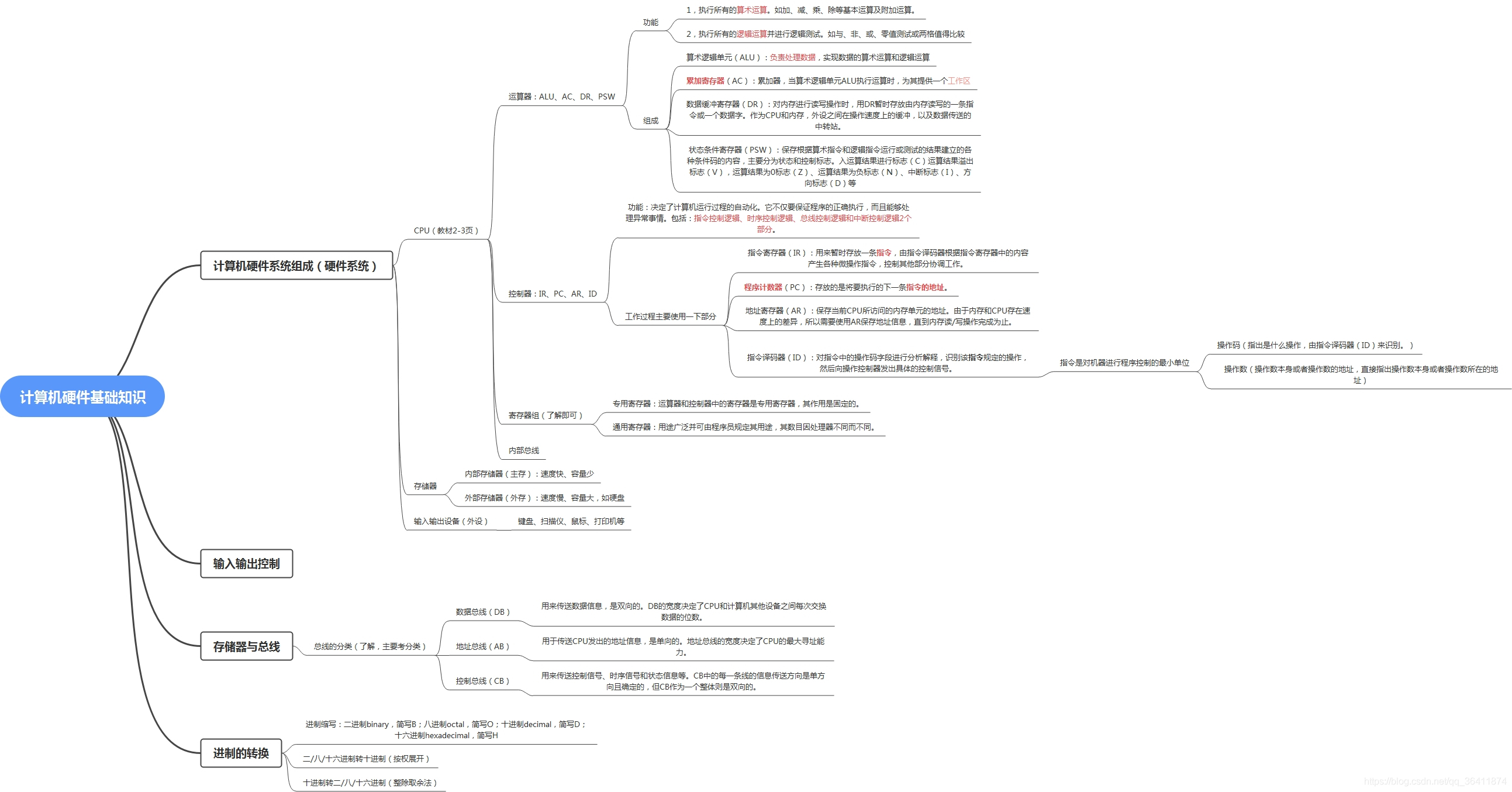
CPU的考点:组成,运算器的组成,控制器的组成
真题练习
例题:计算机中CPU对其访问速度最快的是( )。
A. 内存 B. Cache C. 通用寄存器 D. 硬盘
答案:B
例题:CPU中不包括( )
A.存储器地址寄存器MAR B.指令寄存器 C.地址译码器 D.程序计数器
答案:C
解析:C是存储器的一部分,作用是将地址信号翻译成存储单元的选通信号。
例题:指令译码是对( ) 进行译码。
A.整条指令 B.指令的操作码字段 C.指令的地址码字段 D.指令的地址
答案:B 解析:指令包括操作码字段和地址码字段,而指令译码器只对操作码字段进行译码,用来确定指令的操作功能。
例题:下列寄存器中,汇编语言程序员可见的是( )
A.存储器地址寄存器MAR B.程序计数器PC C.存储器数据寄存器MDR D.指令寄存器IR
答案:B 解析:汇编程序员可以用转移指令、子程序调用指令等设置PC的值,故PC可以被程序员看见。而IR/MAR/MDR是CPU内部工作寄存器,对程序员不可见。
例题:在CPU中,常用来为ALU执行算术逻辑运算提供数据并暂存运算结果的寄存器是()。
A. 程序计数器 B. 状态寄存器 C. 通用寄存器 D. 累加寄存器
例题:三总线结构的计算机总线系统由 ( ) 组成。
A. CPU总线、内存总线和IO总线 B. 数据总线、地址总线和控制总线
C. 系统总线、内部总线和外部总线 D. 串行总线、并行总线和PCI总线
例题:属于CPU中算术逻辑单元的部件是( )。
A. 程序计数器 B. 加法器 C. 指令寄存器 D. 指令译码器
例题:CPU中( )不仅要保证指令的正确执行,还要能够处理异常事件。
A. 运算器 B. 控制器 C. 寄存器组 D. 内部总线
答案: B
例题:微机系统中,( )不属于CPU的运算器组成部件。 A.累加寄存器 B.程序计数器 C.多路转换器 D.ALU单元
例题:指令寄存器的位数取决于( )。
A.存储器的容量 B.指令字长C.数据总线的宽度 D.地址总线的宽度
答案:B
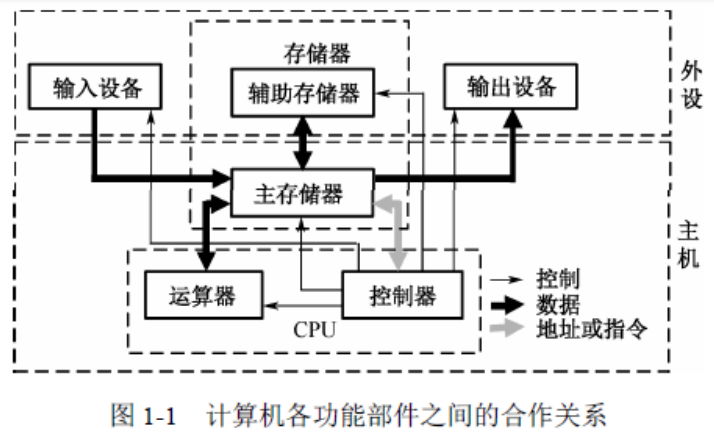
【练习1】如图,冯·诺依曼计算机由五大逻辑部件组成。其中,①和⑤分别是输入设备和输出设备,③和④分别是____和____,②是____。

【练习2】以下关于冯·诺依曼计算机的叙述中,不正确的是( )。 A.程序指令和数据都采用二进制表示 B.程序指令总是存储在主存中,而数据则存储在高速缓存中 C.程序的功能都由中央处理器,(CPU)执行指令来实现 D.程序的执行过程由指令进行自动控制




数据表示
什么是 R 进制
R进制,通常说法就是逢R进1,可以用的数为R个,分别是[0,1,2,…,R-1]。例如十进制数的基数为10,即可以用到的数码个数为10,它们是[0,1,2,3,4,5,6,7,8,9]。二进制数的基数为2,可用的数码个数为2,它们是0和1。对于十六进制,它的数码为[0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F]。
为了把不同的进制数分开表示,避免造成混淆,通常采用下标的方式来表示一个数的进制,如十进制数88表示为:(88)10,八进制数76表示为:(76)8。在计算机专业术语的表达中,通常在数字的后面加大写"H"表示十六进制,或在开头加0x,例如 FCH或0xFC就表示十六进制数FC。
二进制数是计算机进行计算的基本进制,任何数据都会转换成二进制进行运算,它能方便地通过0和1两种状态表示各种数值,这使得逻辑电路的设计简洁。尽管计算机底层使用二进制计算,但是为了便于程序员们书写和记录,在计算机程序中,我们也会使用二进制、八进制、十进制和十六进制。所以我们要掌握的是这4种进制之间的数据转换方法。
进制的转换
R转十进制
对于 R 进制,如果要实现与十进制的转换,则使用 按权展开法,其具体操作为:
将
R进制数的每一位数值用 $R^k$ 的形式表示,即幂底数为R,指数为k,k与该位和小数点间的间距有关。当该位位于小数点左边时,k则是该位和小数点之间数码的个数;而当该位维语小数点右边时,则k是负值,其绝对值为该位和小数点之间数码的个数加1。
比如二进制和十进制之间的转换: $10111.01 = 1* 2^4+12^2+12^1+12^0+12^{-2}$。
再比如七进制和十进制之间的转换:$403.02 =47^2+37^0+2*7^{-2}$。
十进制转R进制整数-除R取余法
十进制数转其他进制都是除以要转的进制数取余数
例如:十进制 转 二进制:使用除二取余法
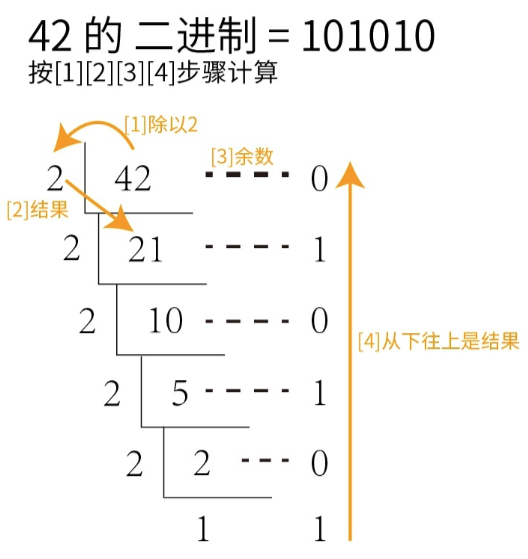
十进制转R进制小数-乘R取整法
小数与整数相反,小数是乘R取整。如果忘记了小数的转换法则,记住是和整数相反的操作即可。
例如:0.625 -》二进制?
0.625 * 2 = 1.25 = 0.25 + 1 |读数
0.25 * 2 = 0.5 = 0.5 + 0 |顺序
0.5 * 2 = 1 = 0 + 1 |从上往下 = 101
结果:0.625 -》0.101
注意:乘到小数部分为0就终止,如果永远不能为0,就需要做出四舍五入按照要求保留小数位数
M进制转N进制
经由十进制转换
可先将M进制转为十进制,再由十进制转为N进制(但是二进制和八进制、二进制和十六进制可以直接转换)
二进制转八进制
八进制数最大是7,也就是111,只有三位,所以 二进制转八进制的时候,只要从低位向高位一次三个数一组,分开,不够三个的用0补齐,小数同理,然后计算三个数下对应八进制的值就可以了。
例如:01101-》001 101-》1 5-》15
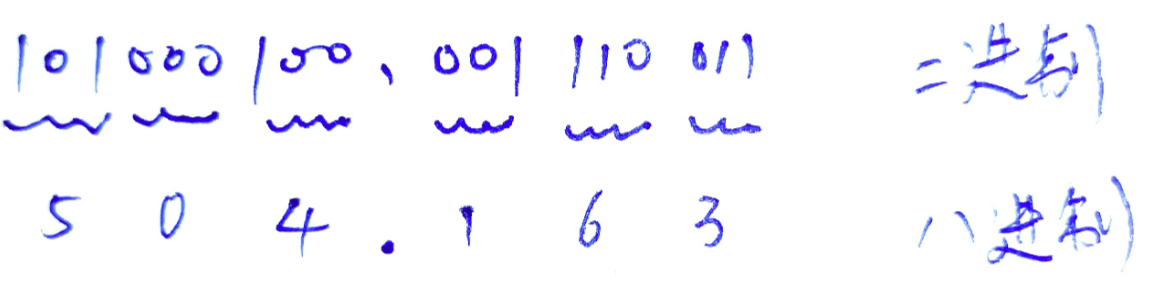
二进制转十六进制
每四位二进制数转换为一位十六进制数,如果二进制数位个数不是四的倍数,整数部分则在最前面补0,小数部分不足则在后面补0。
如二进制数101101有六位,前面补2个0就有八位,为0010 1101,每四位转换为一位十六进制数,如下: 0010-》2,1101-》13》D 最后的结果为:2D
码制
计算机中,无论我们要存储任何数据,它都会转换为二进制码进行存储。现在的计算机中,如果我们要进行加法运算操作,那么我们很容易实现,因为现在的计算机体系大多采用冯诺依曼所提出的经典计算机体系结构,其中就包含了加法运算器。但如果我们要进行减法运算,那么此时就犯难了。没有减法运算器,我们要如何实现减法运算呢?而针对这一问题,原码、反码、补码就产生了。我们常用这三种码来表示一个机器数,从而解决计算机做减法的问题。下面是几个数的实例,下面就分别来看看几种不同表示法的具体知识。
机器数:2进制数,8位表示,不足时需要补位,小数点则隐含,不占位置。
机器数有无符号数和带符号数。无符号数表示正数,没有符号位,带符号数最高位为符号位,正数符号位为0,负数符号位为1。带符号数表示法如下:
| 1 | -1 | +0 | -0 | |
|---|---|---|---|---|
| 原码 | $0000 0001$ | $1000 0001$ | $0000 0000$ | $1000 0000$ |
| 反码 | $0000 0001$ | $1111 1110$ | $0000 0000$ | $1111 1111$ |
| 补码 | $0000 0001$ | $1111 1111$ | $0000 0000$ | $0000 0000$ |
符号位
正式了解不同码制之前,我们先来看看符号位的定义。所谓符号位,是在内存中存放的最左边的一位,如果该位为 $0$,那么说明这个数表示的是正数;而假如该位为 $1$,那么就说明这个数表示的是负数。
原码
是一种最简单的机器数表示法,我们常用最高位来表示符号位,而用余下的其他位来存放该数二进制的绝对值。也即除开符号位之外,原码的数据位就是一个数的二进制绝对值表示。
在上面的示例中,我们发现,虽然 $0$ 和 $-0$ 的原码不一致,但是主要还是符号位的不同,我们再用上面的示例来进行运算:
0001 + 0010=0011,1 + 2 = 30001+0010=0011,1+2=3
0000 + 1000= 1000,0 + (-0)=-00000+1000=1000,0+(−0)=−0
0001+1001=1010,1+(-1)=-20001+1001=1010,1+(−1)=−2
可以发现,如果我们只是进行正数之间的加法运算,是不会出现问题的。但一旦出现正负数相加的情况,就会导致错误结果,而这主要是因为符号位所引起。那有没有相应的解决办法呢?别着急,我们接下来去看看反码。
反码
虽然原码很简单,但是存在的最大问题在于如果一个数加上其相反数结果不为 $0$,即 $1 + (-1)$ 的结果不为 $0$,为了解决这个问题,才有了反码的出现。而针对反码,这里也分为两种情况:
- 如果一个数是正数,那么其反码和原码一样,如 $1$ 的原码和反码均为 $0001$。
- 如果一个数是负数,那么其反码就是其原码除符号位之外,按位取反。如 $-1$ 的原码为 $1001$,其反码为 $1110$。
这个时候我们再来看看原码中存在的问题:
0001+1001=1111,1+(-1)=-00001+1001=1111,1+(−1)=−0
可以看到通过使用反码,我们解决了源码中两个相反数之和不为 $0$ 的情况,但是不是就代表我们可以用反码来进行通用减法运算呢?我们来试试两个不同的负数相加:
1110+1100=1010,(-1)+(-3)=-51110+1100=1010,(−1)+(−3)=−5
就离谱,这结果明显错误!所以反码还是不能彻底解决减法运算的问题。而相应的,科学家们又提出了补码这一概念。
补码
同样的,补码也很特殊,针对正负数也分为了两种情况:
- 如果一个数是正数,那么该数的补码等于其原码,如 $1$ 的原码和补码均为 $0001$。
- 如果一个数是负数,那么该数的补码等于反码 $+1$,如 $-1$ 的反码为
1110,那么其补码即为1111。
同样,我们来试试看反码中进行减法运算所出现错误的情况:
1111+1111=1110,(-1)+(-1)=-21111+1111=1110,(−1)+(−1)=−2
诶,完美解决了反码中两个负数相加时所出现的结果错误的情况。因此在计算机中,为了避免运算错误,都是采用的补码进行加减法运算。
不同码制之间的转换总结
经过上面的各种码制介绍之后,我们将一个数的不同码制之间的转换规律总结如下图:
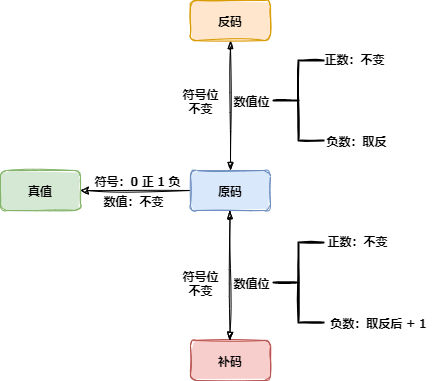 移码
移码移码
除开常用的原码、反码、补码之外,还有一种码制叫做移码。所谓移码,又叫做增码或者偏置码,它是在数 $X$ 上增加一个偏移量来定义的,通常用来表示浮点数的阶码,其表示形式类似于补码,只是其符号位用 $1$ 来表示正数,$0$ 来表示负数,则数值表示部分则是与补码相同。
| 1 | -1 | +0 | -0 | |
|---|---|---|---|---|
| 原码 | $0000 0001$ | $10000001$ | $00000000$ | $10000000$ |
| 反码 | $00000001$ | $11111110$ | $00000000$ | $11111111$ |
| 补码 | $00000001$ | $11111111$ | $00000000$ | $00000000$ |
| 移码 | $10000001$ | $01111111$ | $10000000$ | $00000000$ |
| 类型 | 正数 | 负数 |
|---|---|---|
| 源码 | 不足8位补0,最高位必须是0 | |
| 反码 | 不足8位补0,最高位必须是1 | |
| 补码 | ||
| 移码 |

